FRACTIONS
What is a Fraction?
A fraction is a number that represents a part of an entire group.
Note: Each part is equal in size.
Fractions are written in
the form
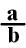or a/b,
where a and b are whole numbers
and the number b is not 0. The preferred notation is generally
.
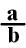The top number a is called the numerator. The bottom number b is called the denominator.
The numerator (top
number) tells you how many parts you have. The denominator (bottom
number) tells you the total number of possible parts. Another way to look
at this is that the denominator tells you how many parts are in a whole.
For instance, if a pizza is sliced into 8 equal parts, that is the number in
the denominator. If you eat two slices of pizza the numerator would be
2. The fraction would be written
.
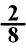MULTIPLYING FRACTIONS
Multiplying fractions is easy!
THE RULE:
Simply multiply the top numbers, and then multiply the bottom numbers. The denominators do not need to be the same.
EXAMPLES:
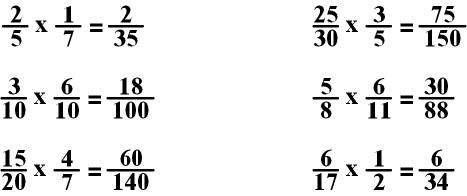
Let’s try a couple problems together!
Practice
1:
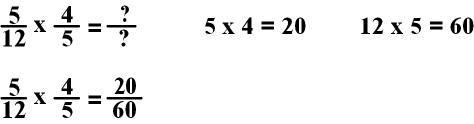
Practice
2:
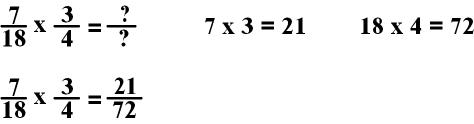
Sometimes when you are multiplying fractions the numbers are large and difficult to calculate in your head, so we find ways to make it easier.
EXAMPLE:
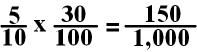
In this example there are two ways I can simplify these terms.
In the fraction
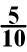, I can divide both numbers by 5.
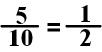
In the fraction
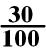, I can divide both numbers by 10.
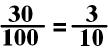
Now it is easier for me
to multiply these fractions!
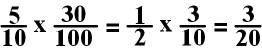
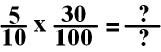
The numbers 10 and 30 can
both be divided by 10. In this case, both 5 and 100 can be divided by 5.
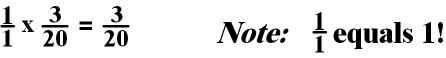
Why can we do this?
This can be done because the numbers cancel each other out. Let me show
you how.
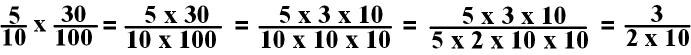
Let’s try a couple problems together!
Practice
3:
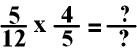
There is no integer (whole number) that I can divide both the numerator and the denominator of either fraction. However, I can take the numerator of one fraction and the denominator of the other fraction and simplify.
The 5 in the numerator of
the first fraction and the 5 in the denominator of the second fraction can both
be divided by 5.
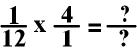
The 4 in the numerator of
the second fraction and the 12 in the denominator of the first fraction can
both be divided 4.
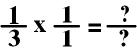
Now it is easy for me to
multiply these fractions!
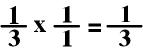
Practice
4:
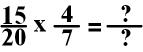
I can divide both the numerator
and the denominator of the first fraction by 5. There is no integer
(whole number) that I can divide both the numerator and the denominator of the
second fraction.
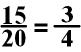
Now the multiplication of
the two fractions is easier!
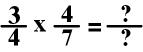
I can further simplify
this equation by using the numerator of second fraction and the denominator of
the first fraction. Both of these numbers (4 and 4) can be divided by
4. There no integer (whole number) that I can divide both the first
numerator and the second denominator (3 and 7).
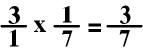
I could have also
simplified the original equation by using the numerator of second fraction and
the denominator of the first fraction. Both of these numbers (4 and 20)
can be divided by 4. There no integer (whole number) that I can divide
both the first numerator and the second denominator (15 and 7).
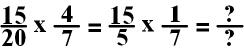
I can further simplify this
equation by simplifying the first fraction by dividing both 15 and 5 by
5. There is no integer (whole number) that I can divide both the
numerator and the denominator of the second fraction.
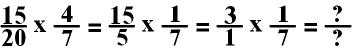
Now it is easy for me to
multiply these fractions!
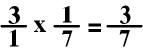
Practice
5:
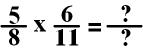
There is no integer (whole number) that I can divide both the numerator and the denominator of either fraction.
Note: In each fraction, one of the numbers is odd and the other is even.
However, I can take the
numerator of the second fraction and the denominator of the first fraction and
simplify. Both can be divided by 2.
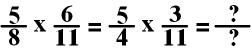
Again the multiplication
of the two fractions is easier!
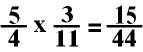
DIVIDING FRACTIONS
Dividing fractions is also simple!
THE RULE:
Take the
reciprocal of the second fraction and multiply it to the first fraction.
The reciprocal of a fraction is the numerator and denominator flipped.
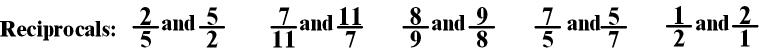
Note: A fraction
multiplied by its reciprocal equals 1!
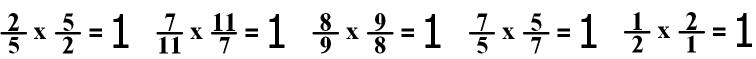
EXAMPLES:
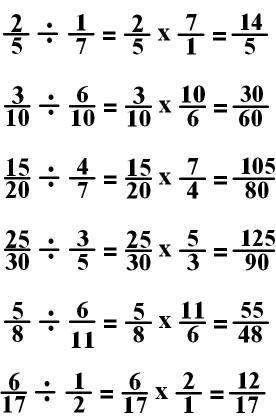
Let’s try a couple problems together!
Practice
1:
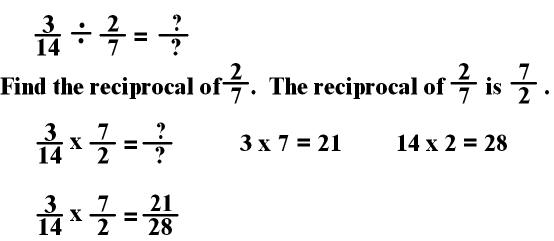
Practice
2:
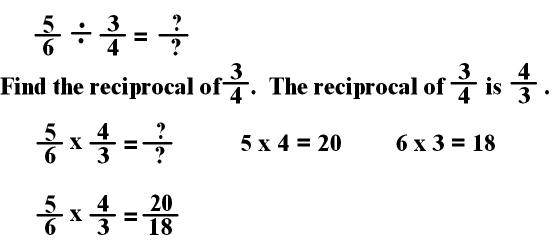
ADDING AND SUBTRACTING FRACTIONS
Addition and Subtraction are opposite operations.
Addition means to group things together.
Subtraction means to take something away from a group.
Addition and Subtraction follow the same rule for working with fractions.
THE RULE:
You can only add or subtract fractions that have the same denominator (bottom number).
EXAMPLES:
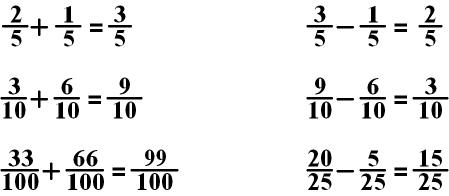
If both of the fractions you are trying to add or subtract have the same denominator (bottom number), for your answer you keep the same denominator (bottom number) and add or subtract the two top numbers (the numerators).
This is all there is to adding or subtracting fractions! The next section will teach you what to do when the denominators are not the same.
How to Make Denominators the Same
Often you are asked to add or subtract denominators that are different. Since the denominators must be the same in order to perform the operations of addition or subtraction, you must convert one or both of the fractions.
EXAMPLE:
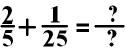
In the above equation, I would
choose to change 2/5 into a fraction with 25 in the
denominator. I would do this by multiplying both the numerator and
denominator by 5.
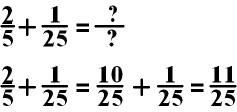
Why can I do this? I can do this because I have not changed the value of the fraction, but I have changed the way the fraction looks. I have not changed the value because 5/5 equals 1. One times any number equals that number.
Examples:
1 x 3 = 3
19 x 1 = 19
9 x 1 = 9
79 x 1 = 79
Back to the original
equation:
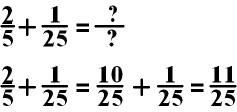
Let’s try some conversions together!
Practice
1:
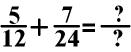
In the above equation, I
would choose to change 5/12 into a fraction with 24 in
the denominator. I would do this by multiplying both the numerator and
denominator by 2.
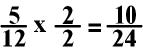
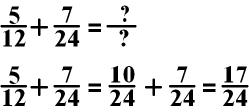
Practice
2:
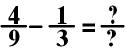
In the above equation, I
would choose to change 1/3 into a fraction with 9 in the
denominator. I would do this by multiplying both the numerator and
denominator by 3.
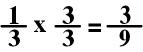
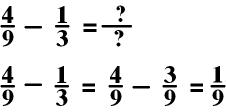
Practice
3:
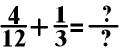
You can also use division to convert a fraction, however, both the numerator and the denominator must be divisible by the number.
In the above equation, I
would choose to change 4/12 into a fraction with 3 in the
denominator. I would do this by dividing both the numerator and
denominator by 4.
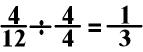
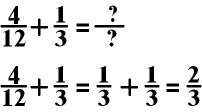
Practice
4:
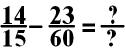
In the above equation, I
would choose to change 14/15 into a fraction with 60 in
the denominator. I would do this by multiplying both the numerator and
denominator by 4.
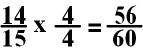
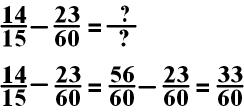
What if there is no number to multiply one of the denominators to change to the other denominator? You can multiply the first fraction by the denominator of the second fraction and multiple the second fraction by the denominator of the first fraction.
Practice
5:
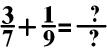
In the
above equation, you multiple the first fraction 3/7 by 9/9
and the second fraction 1/9 by 7/7.
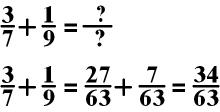
Practice
6:
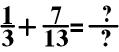
In the
above equation, you multiple the first fraction 1/3 by 13/13
and the second fraction 7/13 by 3/3.
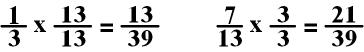
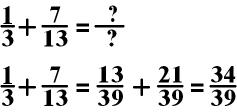
Practice
7:
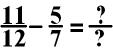
In the
above equation, you multiple the first fraction 11/12 by 7/7
and the second fraction 5/7 by 12/12.
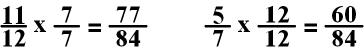
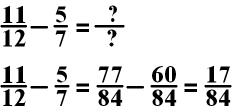
Practice
8:
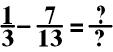
In the
above equation, you multiple the first fraction 1/3 by 13/13
and the second fraction 7/13 by 3/3.
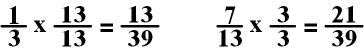
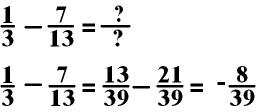
Notice that the answer is a negative fraction. The rules for adding and subtracting whole numbers also apply in these operations with fractions. 13 – 21 = (13) + (-21) = -8
When trying to add two numbers with different signs, you subtract the smallest from the largest and take the sign of the largest.
MIXED NUMBERS AND IMPROPER FRACTIONS
What is a Mixed Number? A Mixed Number has an integer and a fraction.
EXAMPLES:
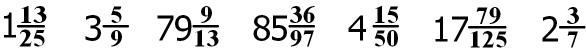
Sometimes we cannot perform the operations of addition and subtraction with mixed numbers because the denominators of the fractions are not the same. I can add or subtract integers. I can also add or subtract fractions with the same denominator.
We can never perform the operations of multiplication and division with mixed numbers, so we must change them to improper fractions.
What is an Improper Fraction? An Improper Fraction is a fraction in which the numerator is larger than or equal to the denominator.
EXAMPLES:
You convert a mixed number to an improper fraction by multiplying the integer by the denominator and adding that value to the numerator.
EXAMPLES: Mixed
Numbers à Improper Fractions
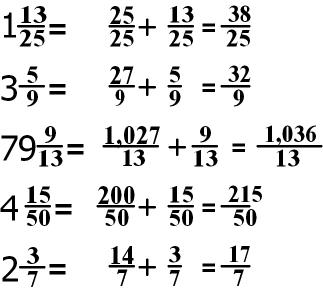
Now try converting a few mixed numbers to improper fractions!
Practice
1:
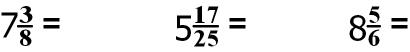
You can convert an improper
fraction to a mixed number or an integer, easily by dividing the numerator by
the denominator.
EXAMPLES:
Improper Fractions à Mixed Numbers
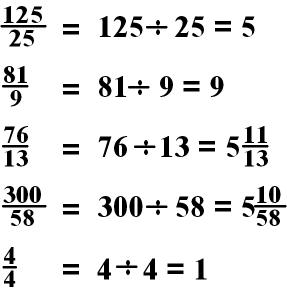
Now try converting a few improper fractions to mixed numbers!
Practice
2:
The preferred way of expressing fractions is simplest form. In the next section, I will teach you to simplify fractions.
A Mixed Number is acceptable, as long as the fractional part is expressed in its simplest form.
We do not want improper fractions for answers. We only use improper fractions for calculations.
CONVERTING AND SIMPLIFYING FRACTIONS
In the previous examples of how to add, subtract, multiply and divide fractions, I did not focus on reducing the answer to its simplest form. I will now teach you to simplify fractions.
An Equivalent Fraction is a fraction of the same value that looks different.
EXAMPLES:
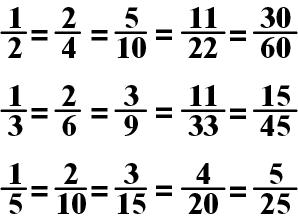
In each group of fractions above, each fraction represents the same amount (the value is the same), but looks different (are comprised of different numbers). The first fraction of each group is the simplest form. It is not the simplest form because the numerators are one. It is the simplest form because the numerators and the denominators cannot be divided by any common number.
There are several ways to convert and simplify fractions.
Note: Integers can be converted to fractions by placing them over 1. (2 = 2/1 15 = 15/1)
Let me show you how I
quickly simplify a fraction using division!
The first thing I do is
determine whether the denominator can be divided by the numerator. If so,
this is the quickest way to the simplest form. 60 can be divided by 20,
so I divided both the numerator and the denominator by 20.
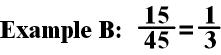
The first thing I do is
determine whether the denominator can be divided by the numerator. If so,
this is the quickest way to the simplest form. 45 can be divided by 15,
so I divided both the numerator and the denominator by 15.
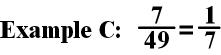
The first thing I do is
determine whether the denominator can be divided by the numerator. If so,
this is the quickest way to the simplest form. 49 can be divided by 7, so
I divided both the numerator and the denominator by 7.
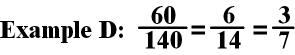
The first thing I do is determine whether the denominator can be divided by the numerator. 140 cannot be divided by 60 evenly giving me a whole number. Next I find the biggest number I can think of that I can divide both the numerator and the denominator. I’ve chosen the number 10. I need to simplify further, because I can see that both of these numbers are even and, therefore, can be divided by 2. Three-sevenths is the simplest form because there are no more whole numbers that I can divide each of these numbers by. Both of these are prime numbers.
Note: A Prime Number is a whole
number greater than one that can only be divided by 1 and itself. (2, 3,
5, 7, 11, 13, 17, 19…)
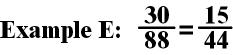
The first thing I do is determine whether the denominator can be divided by the numerator. 88 cannot be divided by 30 evenly giving me a whole number. Next I find the biggest number I can think of that I can divide both the numerator and the denominator. I couldn’t think of a large number, but I see that both numbers are even, so they both can be divided by 2. I can’t simplify further because 15 can only be divided by 3 and 5. 44 cannot be divided by either 3 or 5, so there are no more common factors.
Now you try to simplify some fractions!
Practice:
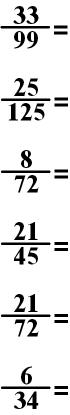
CONVERTING FRACTIONS TO DECIMALS
There are two methods for converting fractions to decimals.
(10, 100, 1,000…) Then write in decimal form.
IMPORTANT NOTE: Fractions are division equations! The numerator is being divided by the denominator!
Examples
– Method 1:
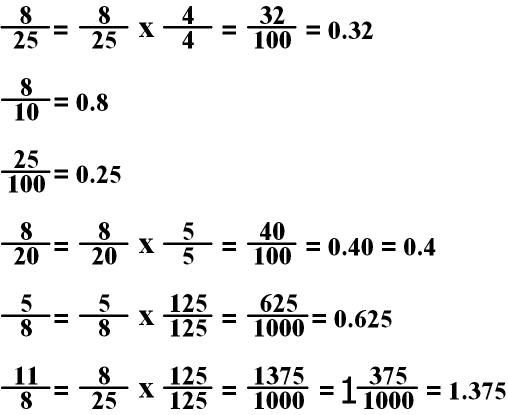
Examples
– Method 2:
This is my preferred method, especially if I can use a calculator!
Practice:
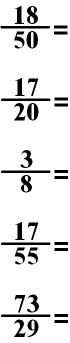
COMPARING FRACTIONS
If the denominators are
the same, the fraction with the largest numerator is the largest fraction.
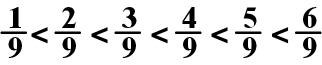
If the numerators are the
same, the largest fraction is the one with the smallest denominator. The
whole sectioned into the fewest parts has the largest parts.
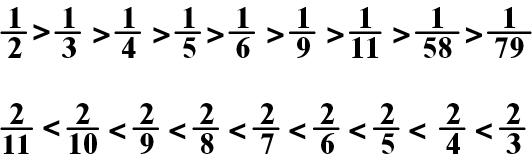
If the numerators and
denominators are not the same, change one or both of the numerators to the same
numerator by multiplying (or dividing) by some number. Remember to
do the same thing to the denominator! Whatever you do to one part
of the fraction, you must do to the other part in order to maintain the value
of the fraction. You want to maintain the value of the fraction but
change the way it looks for calculations.
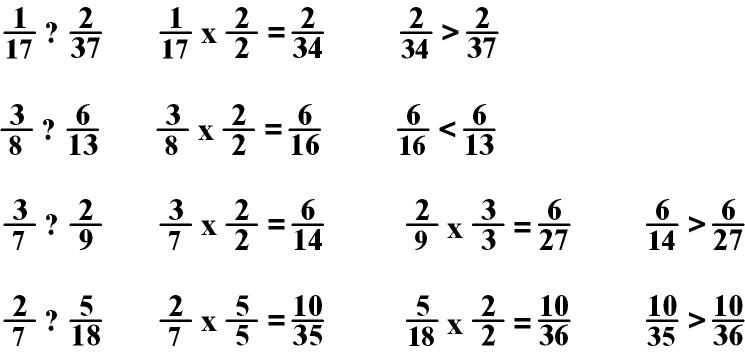
You can also use this procedure to make the denominators the same and then compare the numerators.
If the numerators and denominators are not the same, change one or both of the denominators to the same denominator by multiplying (or dividing) by some number. Remember to do the same thing to the numerator! Whatever you do to one part of the fraction, you must do to the other part in order to maintain the value of the fraction. What you are doing is creating an equivalent fraction. You want to maintain the value of the fraction but change the way it looks for computations.
Please try the following practice problems now.
CROSS MULTIPLICATION
What is Cross Multiplication?
Cross Multiplication is a
way to check whether two fractions are equal. It is also a way to set up
and equation to find the value of one unknown (numerator or denominator), as
long as you have the other three values.
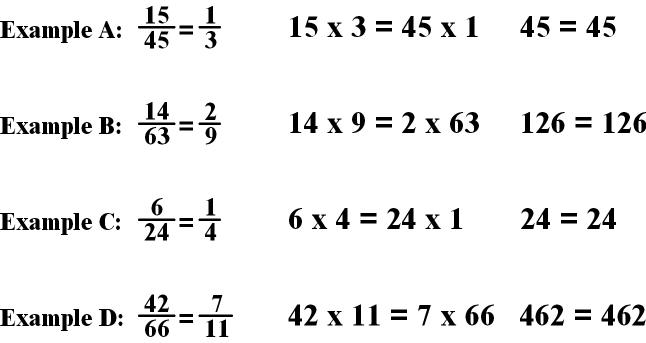
Solving for an
Unknown
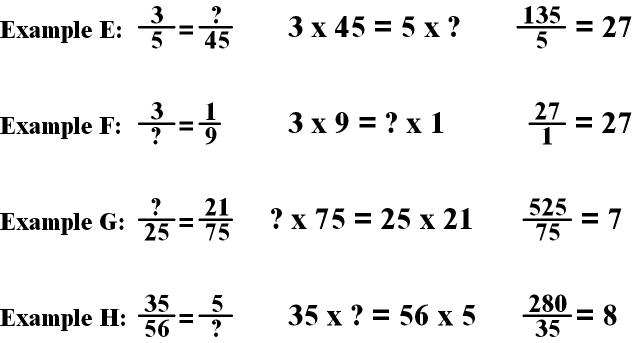
Now you try these
problems!
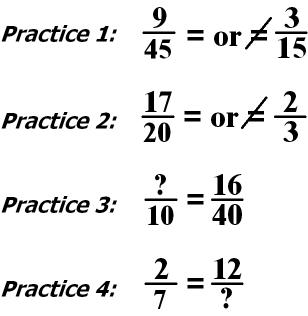
COMPLEX FRACTIONS
What is a Complex Fraction?
A complex fraction is a fraction whose numerator and/or denominator is also a fraction or mixed number.
EXAMPLE A:
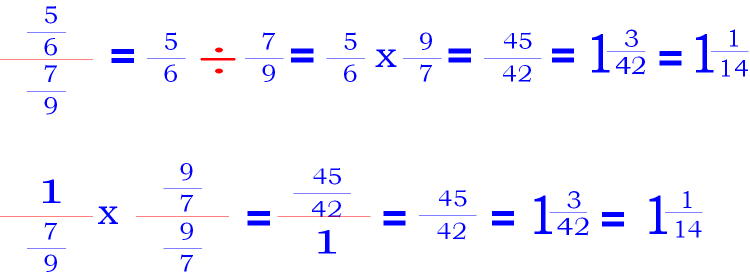
EXAMPLE B:
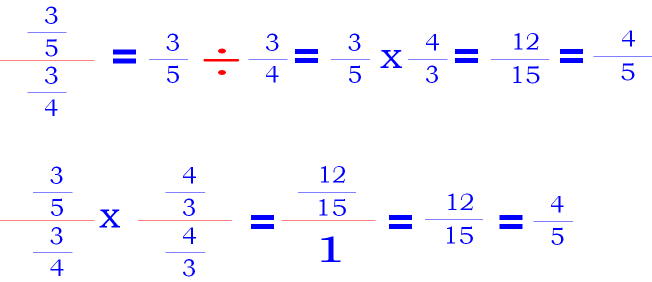
When working with complex fractions, if the numerator or the denominator is a whole number, convert the whole number to a fraction.
Note: Integers can be converted to
fractions by placing them over 1. (2 = 2/1
15 = 15/1)
EXAMPLE C:
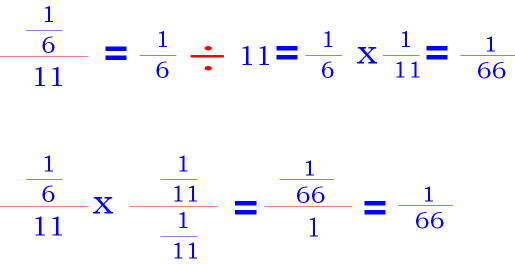
EXAMPLE D:
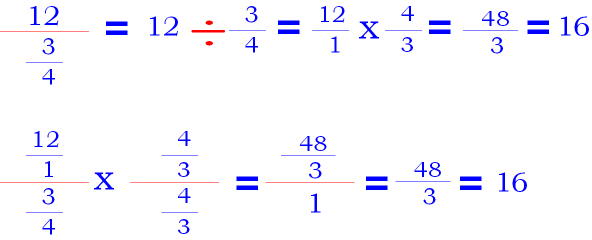
FINAL
PRACTICE!!!
YOU ARE FINALLY FINISHED WITH THIS LESSON!
This lesson is extremely long! I suggest you listen to this lesson over two to four days. Learn one topic per day, if you have the time. All of this can be learned in one day if necessary. However, it is not advisable to try and jam new information into your brain for more than two hours. You want to learn this material, not have temporary memory of these topics.
Hopefully I was successful in teaching you to work with fractions. Please go to the website blog and let me know.
The website address is www.mathbeast.com.
Copyright 2008 www.mathbeast.com. All rights reserved.
